When to jump into the water - with maths

I once heard that with the following problem dogs had less of an issue than many distinguished people of the human race.

Consider the following: There is an object in the water at some distance from you. You have a number of choices of how to get there. You could jump straight into the water and swim all the way, or you could run along the shore until the distance to the object is shortest and then jump in. What would you do? Well, as always the truth is somewhere in between! The following pic should illustrate the setup that will be used for this brief Mathematical analysis:

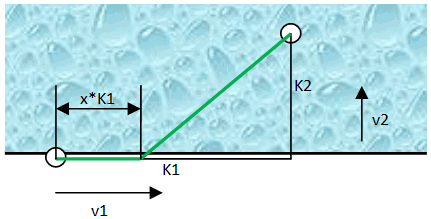
You can see that the distance to the object is given as K1 and K2 while the respective velocities with which you can manage those distances are v1 and v2. I will express the point where you jump into the water as x (such that the distance travelled along the shore is x*K1). Furthermore I will use some ratios, namely z and r as the ratio of the velocities on land and in the water and the ratio between the distance along the shore and the distance from the shore straight to the object in the water, respectively.

z=v2v1,r=k2k1z = \frac{v_2}{v_1}, r = \frac{k_2}{k_1}

Since velocity is distance travelled over time, we will get the time as distance travelled divided by velocity. Now we are equipped to express the total time it takes from your position to get to the object in the water:

Ttotal=f(x)=k1v1x+k1v1z(1−x)2+r2T_{total} = f(x) = \frac{k_1}{v_1} x + \frac{k_1}{v_1 z} \sqrt{(1-x)^2+r^2}

The function that gives us the total time does indeed provide us with a position x somewhere between your origin posn. and the point that faces straight the object in the water where you will reach said spot quickest. Thing is, since on land you’re usually much quicker than in the water, the shortest distance (jumping right into the water) isn’t necessarily the quickest route. Now, when we hear that the function giving us the total time spits out the point at which the total time is lowest, we think local minimum and we have to think of a derivation. After all, when the derivative is 0, the function has a minimum or maximum at that point. So, differentiating (with the aid of the chain rule) gives us:

f′(x)=1+x−1z(1−x)2+r2f'(x) = 1 + \frac{x - 1}{z\sqrt{(1-x)^2+r^2}}

Such that we can find the least amount of time spent on the way with this equation:

1+x−1z(1−x)2+r2=01 + \frac{x - 1}{z\sqrt{(1-x)^2+r^2}} = 0

After some fiddling (and man, I’ve gone bad in Maths, took me 3 attempts to get it right) you get the following polynomial:

x2(z2−1)+2x(1−z2)+z2(r2+1)−1=0x^2(z^2 - 1) + 2x(1-z^2) + z^2(r^2 + 1) - 1 = 0

For this sort of thing, maths has a simple equation that for a polynomial of the form ax2+bx+c you can get values for x where the equation gives us a 0 result:

x=−b±b2−4ac2ax = \frac{-b\pm\sqrt{b^2 - 4ac}}{2a}

When we stick in the values of the found polynomial in this equation and after more fiddling (sigh I told you I was better with this once..?) you arrive at this one here:

x=1±zr2(1−z2)z2−1x = 1 \pm \frac{z\sqrt{r^2(1 - z^2)}}{z^2 - 1}

So roughly, the quicker you are on the land, the more you should walk along the shore, but it depends on the distance, really. In such a situation it is probably best to fire up your Internet and visit the small Javascript calculation form down here. If you have a slow connection and the guy in the water is drowning, do a good guess. Even better, though, would be to check out what your dog does!