Untyped matter and RIM fuelling
Untyped matter – matter that is defined in space and time but does not bear any other characteristics of the 4Band continuum, i.e. it has no electrical charge or strong atomic force ‘colour’, it has no mass and no spin. A volume containing untyped matter may also be described as a vacuum whose inherent energy is much greater than the one encountered in our 4Band universe.
Let us concentrate onto a thin layer just outside of the MRC’s rotating surface. This layer hardly ever reaches thicknesses of about 10-8 m. In this area particles are strongly exposed to the interactions running at greater frequencies inside the MRC. If you consider the kind of particle scattering we obtain in human-made particle accelerators, a set of typed matter can be brought into interaction with another in order to generate a third set of typed matter. In a way, the interactions happening inside this boundary layer are so rapid that the actual types that are members of the interaction sequence are not observable anymore. This is not completely correct but comes close to it. This is the layer in which we find untyped matter. The interactions happening in this layer run too fast to be fully compatible to the typical interaction frequencies that control 4Band physics. This layer can indeed be thought of as a very special type of vacuum. Compare this to the human findings proving the existence of vacuum energy, energy that exists and is quantifiable despite the absence of typed particles.
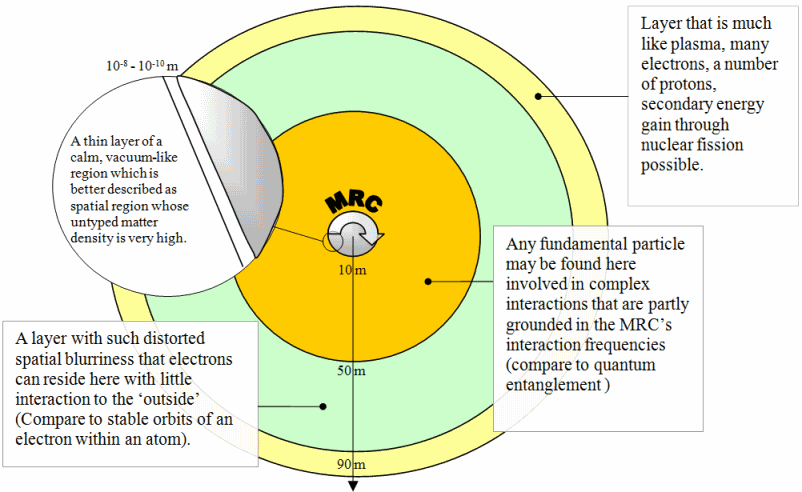
In other words, between the electromagnetic chaos of the RIM’s surface, followed by layers of increased particle entanglement and spatial blurriness and the MRC at the core of the system we find a very thin layer. It is a seemingly calm region that is comparable to a vacuum as we encounter in deep space. Even so, the energy that can be accredited to this zone is extreme.
In terms of considering the complete RIM system, the untyped matter layer plays an extremely important role in augmenting the MRC’s capabilities. It extends the saturation points for the possible particle interactions and type conversions far beyond what is possible in a simple, non-rotating MRC. The layer can be thought of in two ways. It ‘extracts’ spatial representation away from the internal MRC domain, plus, it describes a protective layer surrounding the rotating crystal. Any type imbalances that have been introduced by charging or using the RIM in a certain way are hidden from the interactions that approach more and more the interaction speeds of the 4Band continuum while moving away from the MRC. A type imbalance e.g. in terms of electric charge can thereby be sustained far beyond what is available when using certain resonances on a still, ‘solid’ MRC. This effect can be further increased by exposing more volume of the crystal to the boundary layer of untyped matter, in other words, by increasing the surface-to-volume ratio of the MRC.
Before you ask, this feat is indeed possible with a RIM. In the process of charging a RIM, the multi-resonance crystal undergoes something that can be understood as a change in its state of aggregation. I had previously mentioned that it is rather difficult to imagine the MRC being in a solid state. This is even more so in the excited state that is encountered inside the RIM. By manipulating the containing electromagnetic field, a new shape can be impressed upon the complete RIM. This possibility allows the Iilasian engineers to reshape the complete RIM towards resembling a thin cylinder, thereby increasing the surface-to-volume ratio to numbers beyond those achieved by unexcited MRCs. It is basically impossible to speak of a density of the MRC inside the rotating interaction matrix; nonetheless the total surface that can be covered by an untyped matter boundary layer can also be increased through the process of extending the RIM into a cylinder or into other forms.
Finally it should be noted that the ability of the untyped matter layer to store the spatial representation of potential particles (becoming real particles when it is joined up with type imbalances arising from the MRC) is far greater than the capability of the 4Band continuum to hold typed matter.
When we think about the dimensions of atoms we have to consider spatial dimensions of about 10-10 metres. Even further, the ‘size’ of a proton is taken to be around 10-25 metres, although at those distances the measurement of length looses more and more significance. It is once more difficult to talk about single entities or in fact dimensions within said boundary layer of untyped matter. However, its capability of storing unique elements that, once combined with type information, emerge as particles that interact within the 4Band continuum, is vastly greater than could be achieved by considering dimensions of e.g. atoms. As a rough guide, one can take
- the volume obtained by the boundary layer,* the matter fed into the system during a charging process (which will ideally be similar to the amount of matter obtained during the discharge or utilization phase),
- and a so-called matter abstraction efficiency μA that describes the ratio between the separation of type and spatial representation between the MRC and the surrounding layer of untyped matter.
This results in a number that describes how many particles have been ‘outsourced’ to the untyped matter boundary layer. From this number an average volume per untyped matter ‘particle’ can be calculated. The optimum value of this volume magnitude is what we humans know as the Planck volume*). It describes the situation in which there is an optimum usage of the ‘available space’ just outside the MRC. This optimum volume is denoted by the Ii as Optimum volumetric unit Ωv. Note that volume measurements within the MRC take place ‘below’ the Planck length, as interaction occurring directly on types cannot be undertaken within an interaction domain that depends upon a space-time frame.
Either way, an ideal scenario where the spatial representation of Hadrons and Leptons really just occupy Ωv cannot be achieved with current Iilasian technology. Consider the following example to understand the dimensions involved. If you would be able to store a Baryon like a proton within a Planck volume and resize a Hydrogen atom accordingly, a RIM whose MRC has reached a shape of a cylinder with a radius of 10 and a length of 300 metres would be able to store a number of atoms comparable to the mass of 41’000 Earths!
This is a simplifying calculation, but it gives an idea of the dimensions involved. The biggest ships of the Ii-swarm can indeed store so many atoms that a considerable percentage of the Earth’s mass could be recreated by recombining the untyped matter with the associated types hidden away within the high frequency interaction matrix of the MRC.
Now that the significance of the untyped matter layer for the achievable type imbalances and raw capacity of storing particles is somewhat clarified - what remains is to have a look at how a vast number of particles can be stored in a RIM.
RIM fuelling
In order to understand the fuelling process used by Iilasian ships, a further property of MRCs and in fact RIMs must be introduced. This property is already known in human quantum mechanics as particle entanglement. I already wrote about the fact that a RIM can be reshaped. This reshaping can be done such that two RIMs are created out of a single one. The generated system is indeed entangled such that types and boundary layer ‘densities’ can be teleported from one RIM to the other**). The fuelling process is therefore undertaken by exposing RIM 2 to particle streams, thereby causing type and particle saturation in RIM 1.
The process is illustrated by following diagram.
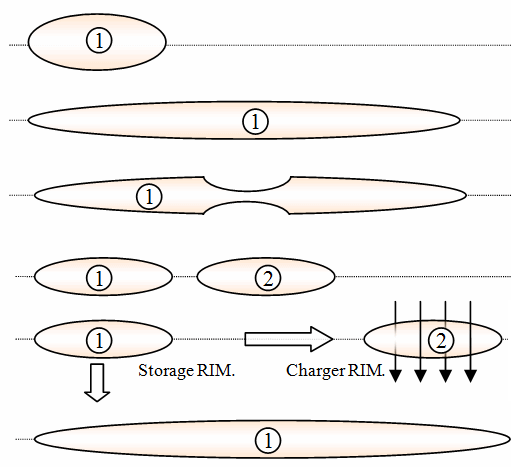
- A RIM is created by the described process
- By manipulating the containing electromagnetic field, the RIM is shaped cylinder-like
- Further corrections to the field while keeping the whole system stable lead to the creation of two RIMs which are causally entangled
- One of the generated RIMs can be exposed to particle streams.* Performing certain manipulations to the electromagnetic field containing RIM 1 now leads to a type any untyped matter transferral from RIM 2 to RIM 1.
The particles required for the fuelling process are obtained by Iilasian ships by entering an orbit around a sun. Here a vast range of different particles can be found, i.e. a great quantity of photons but also numerous electrons, atom cores stripped off their electron shells and more exotic particles like positrons and other counterparts of typical 4Band matter. This helps to save a good mix of differing types and a great total amount of particles into the storage RIM within an acceptable time range.
*)
The Planck length is
The Planck volume is then
Compare this to the approximate volume of an unexcited Hydrogen atom of about
or the approximate volume accredited to a proton of about
**)
By the way, this fundamental property is also the key to the ‘purely causal information transmission’ that is used by the swarm to communicate over distances measured in light-years - this is in fact the major difference to the teleportation known in quantum mechanics where two spatially independent particles are being entangled to be used as a teleport bridge, allowing any teleported information to be read only once. A RIM entanglement is generated from a single spatial entity and allows clearly defined particle bursts in one RIM to be a direct cause of clearly directed particle streams towards the other RIM.