On the fractal nature of effort estimates
We still live in a world where people want to play the game of estimates. Indeed, in some industries this may (kind of) work (Yes, this is the 30th automobile we are designing, and the requirements may be more or less the same (not really) than for the 1st automobile we designed). Alas, in software development we are still regularly in trouble if we try to estimate what it will cost us to finalize some software project.
I am not the first one to compare the creation of software to a hike following some coast-line. Let’s play along, though. Our project needs us to walk around the Lake Constance. First, we have a broad overview of what software we want to build. We look at the lake at the 50km scale of Google Maps:
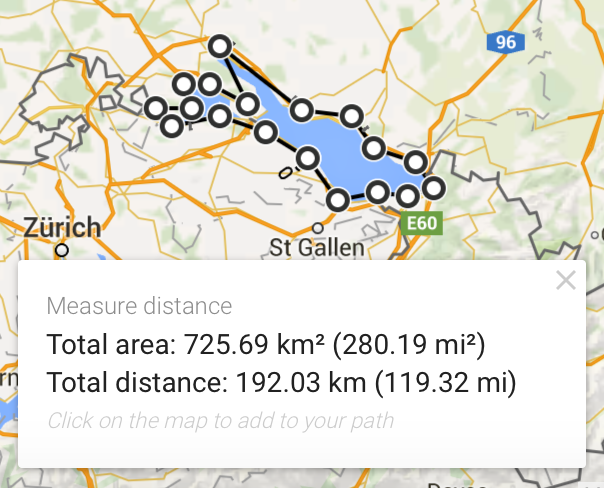
192 km, nice. We start adding more detail, i.e. we look closer to the aim of walking around the lake…
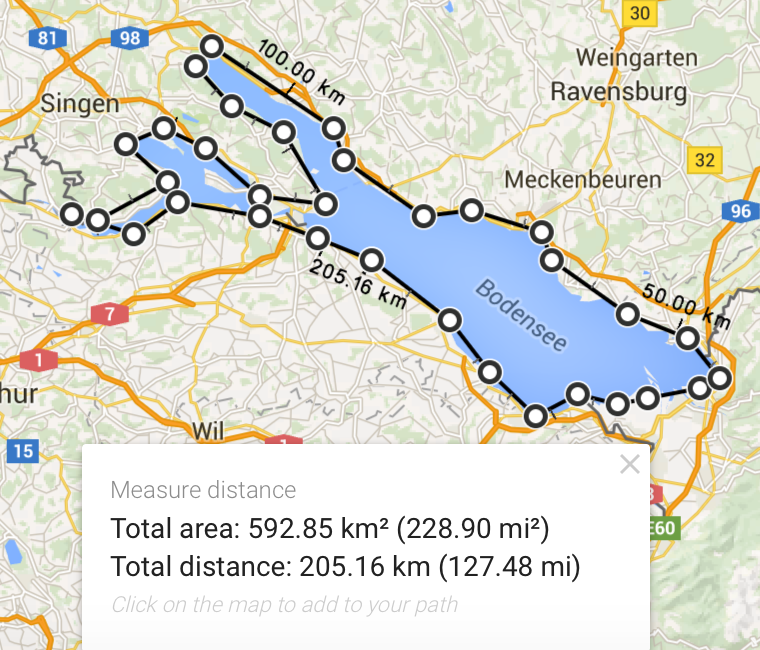
205 km, still on track.
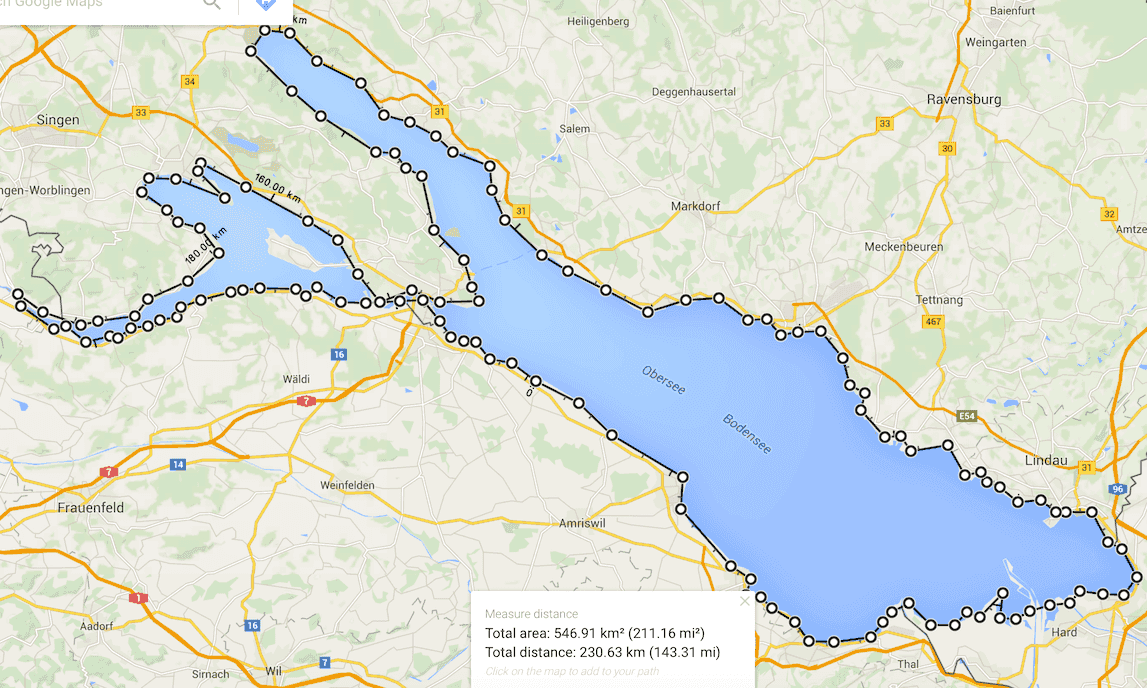
231 km. Only 20% more expensive than the original estimate, looks like we are gaining confidence. We do see that we may be taking some shortcuts for which we could account with some risk percentages.
We decide to start the project…
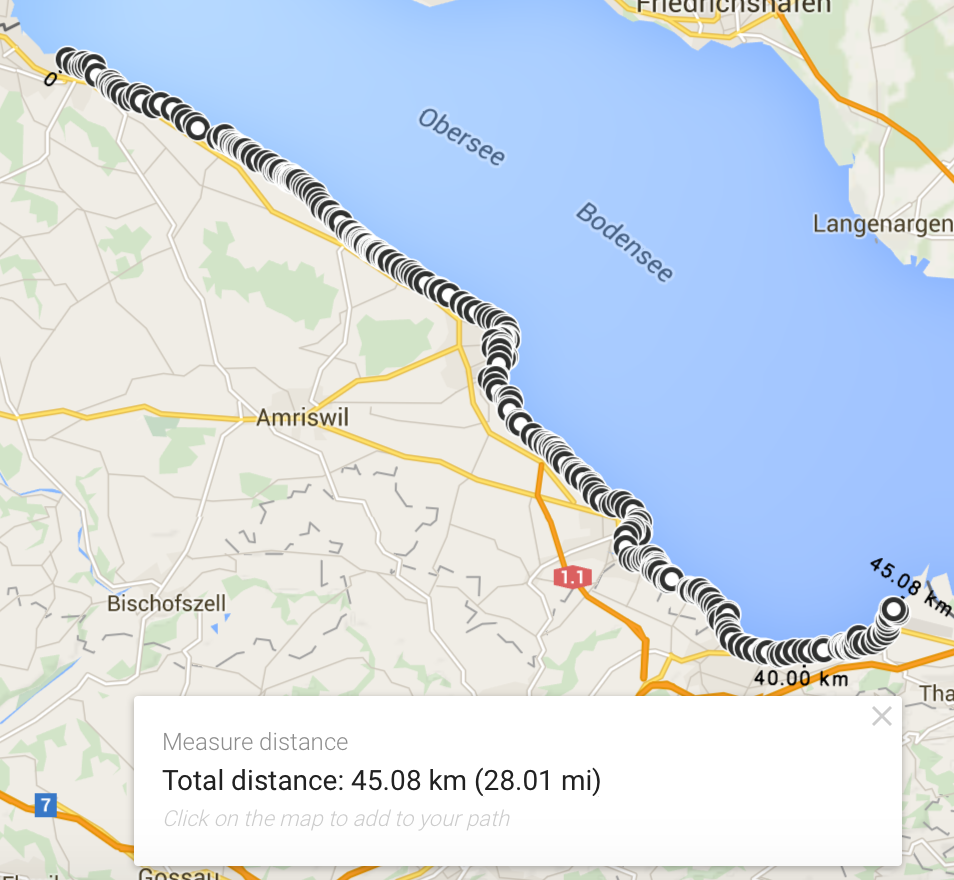
We have burned through almost a quarter of the original budget. 50% more than what we wanted to burn up to now. We also had to make up some additional rules with regard to rivers and the like (we go to the next bridge and cross there).
The next leg then became a total disaster…
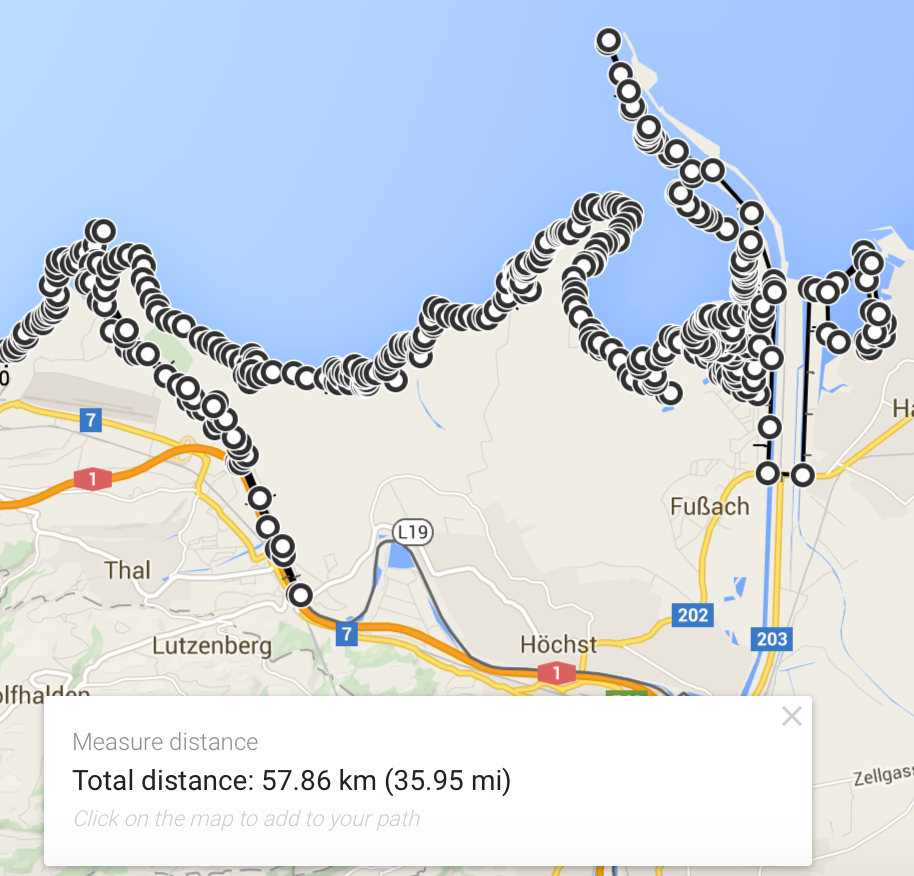
57 km…compare this to the estimate on the 20km scale:
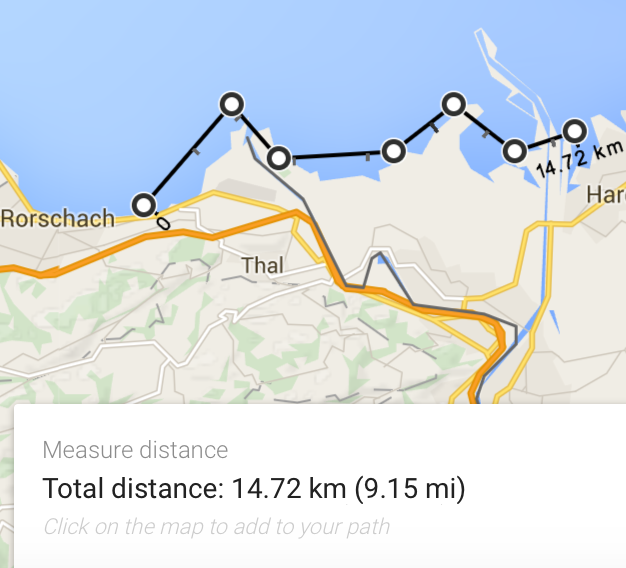
15 km…it took almost 4 times the estimate to cover the desired distance! What happened?!
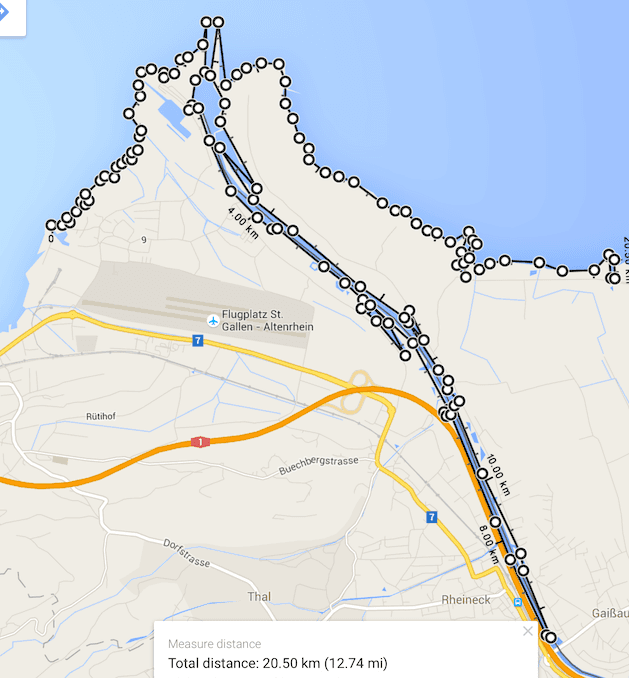
We didn’t find a damn bridge!
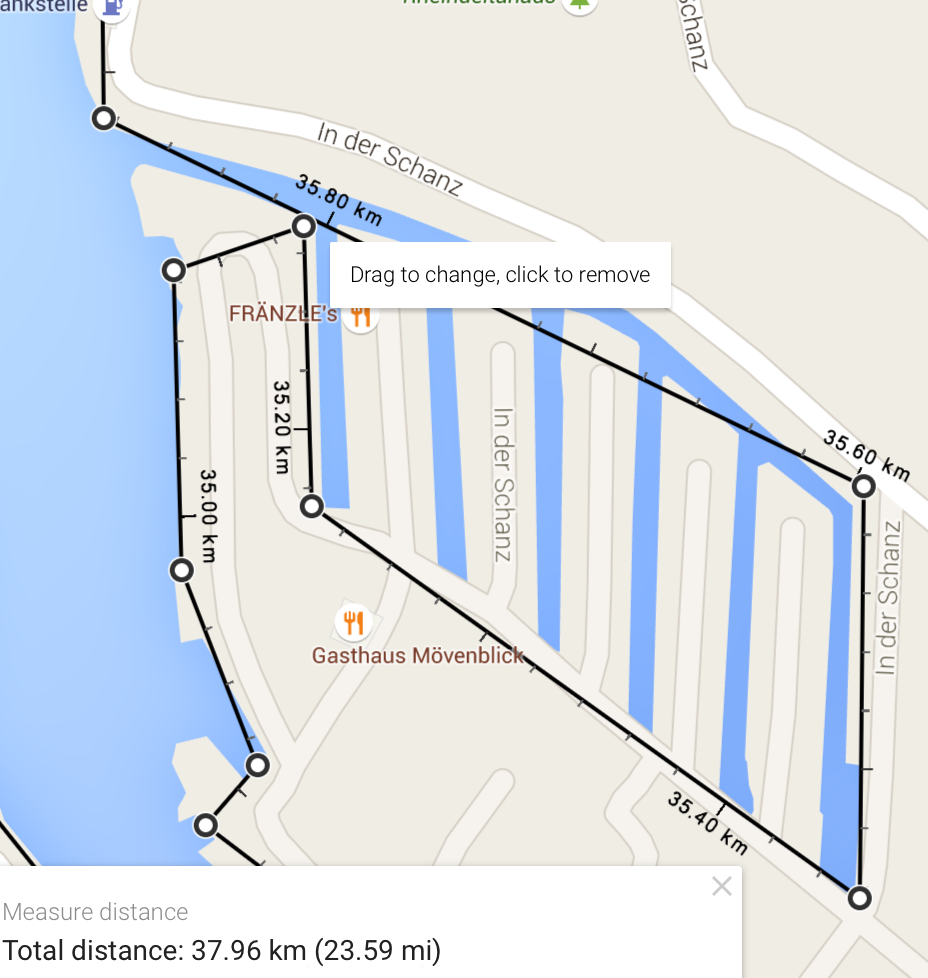
A place where our efforts were about to explode. We took a shortcut!
And so on, and so on. The scope of the project didn’t change, but the expenses are exploding!
Do I see affirmative nods by fellow software developers?
If this metaphor works so well, the question is: Why does it work so well?
It may have to do with the nature of fractals. One of the main characteristics of fractals is that they are self-similar. Zoom into a structure, and you will find additional structures, very similar to the ones you already saw from “higher up”. We find self-similarities in large projects, too. On a large scale, we may draw up necessary activities to get from one place to the other. The activities are inter-dependent. We identify problems for which we provide slack. This happens again and again while we zoom into activities. Some time into the process we will arrive at the point where we don’t see additional value in planning - we will start walking. Whatever detail we put into the planning (Check our 3rd plan of the lake circumference, it looks pretty exact!), it doesn’t protect us from additional activities, inter-dependencies and problems that we did not foresee.
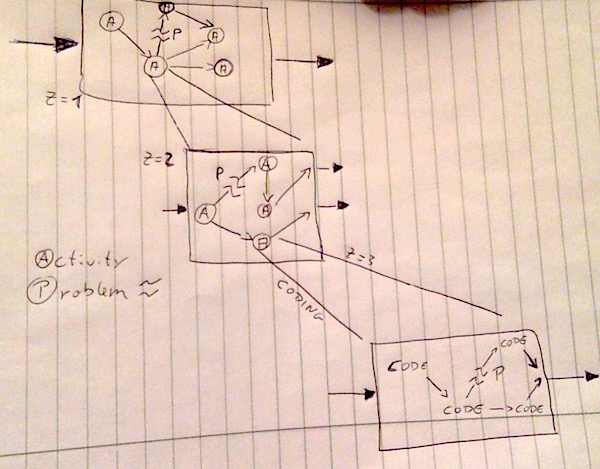
Other things that we haven’t even gotten into, but will probably greatly affect our estimating efforts:
- The effort involved in monitoring the activities (as witnessed by measuring out the distance) grows exponentially.
- In an actual software project, the expected results of the project will inevitably change - In our metaphor this amounts to either a changing coast line, or, when facing the sheer amount of effort required to trace a particular part of the line, to the statement “we will do this later”.
Does all of this information help us in any way? I am not sure. However, especially in the case of tracing coastlines, mathematics has a concept that encapsulates the increase in effort with increasing detail: The fractal dimension. Hence, if there is more to tracing coastlines than being a metaphor to developing software, there may be a chance that the mathematics of fractals can help us in understanding better the capabilities and, more importantly, the inadequacies of estimating efforts in a large software project.