each_cons - the wise and tall of popular languages

A few days ago, Michael Feathers tweeted this:

Now, I am not a complete stranger to ruby, which is why this statement resonated with me, and upon requesting an example, Michael came up with this:

([0] + arr).each_cons(2).count {|x,y| x == 0 && y == 1 }

each_cons is a function that provides consecutive elements of a given list. E.g. [0,1,2,3].each_cons(3).each { |x,y,z| puts "#{x},#{y},#{z}" } It can be useful for obtaining info about the local structure of a list. Think derivatives, rates of change, etc. and probably a host of other things.

This does indeed show off ruby’s expresiveness quite nicely:

The fact that the parameter influences how many items will be yielded into your block reminds us why all of us like to write Javascript once in a while.

What about other languages then?

F#

Let’s look at the code which performs (almost) the same job:

seq { yield 0; yield! {1..4} }
  |> Seq.pairwise
  |> Seq.filter (fun (x,y) -> x = 0 && y = 1)
  |> Seq.length

It is pretty compact and readable, but even though some things look similar, they actually use completely different mechanics of the language

Of note is that pairwise will provide exactly 2 consecutive elements of a list, it does not allow a parameter like the ruby version. This makes sense, since F# is statically typed. If you wanted a version that provides 3 consecutive elements, you would have to write a method yourself that yields an element of type (a,a,a).

C#

To actually achieve the same level of expressiveness we need to put some work into this:

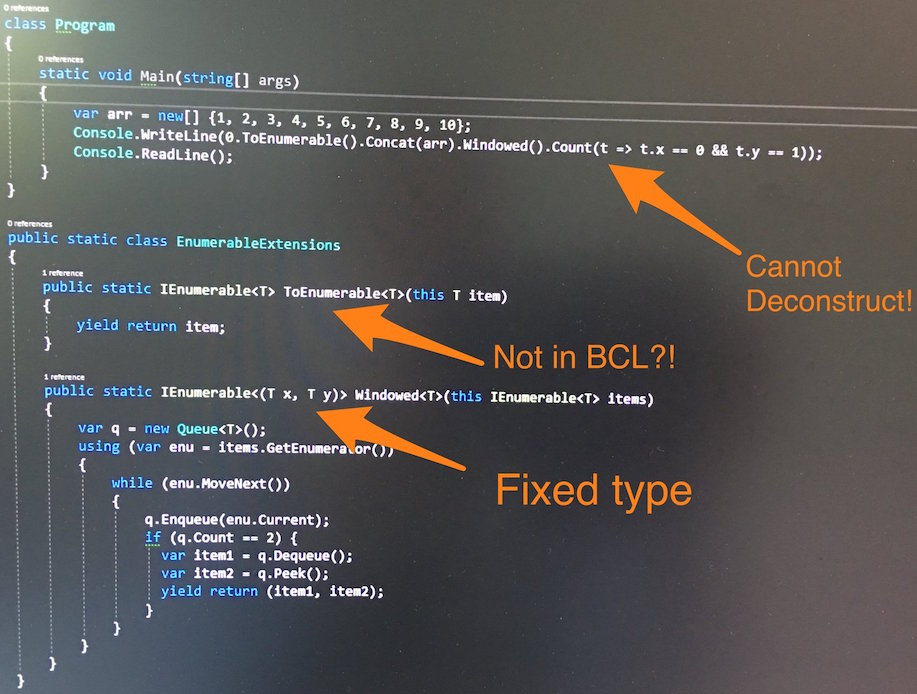
With those two additional extension methods we can now write

0.ToEnumerable().Concat(arr).Windowed().Count(t => t.x == 0 && t.y == 1);

While tuples are now available in c#, you cannot deconstruct them like you can do in most other functional languages or even in ES2016 (which has actually gone to great lengths to make deconstruction a dependable feature).

While I can kind of forgive a missing each_cons-like BCL method, I write the ToEnumerable again in almost every project. I mean, that method is the damned unary return operation!

Kotlin

Xavier Lepaul chimed in with a view on what Kotlin is up to with respect to the challenge:

(listOf(0) + arr).windowed(2).count {(x,y) -> x == 0 && y == 1}

This doesn’t fall very short of the ruby example, however, the windowed is not available yet in Kotlin 1.1 - What I particularly liked is that even though the type signature of windowed is

fun <T> Iterable<T>.windowed(size: Int, step: Int): List<List<T>>

i.e. returning a list of lists, one can still deconstruct the list into the x and y you can see in the lambda provided to count. This works because the deconstruction in kotlin simply starts working when the deconstructed object provides methods named component1 down to componentN. A quick look at Kotlin’s list type…

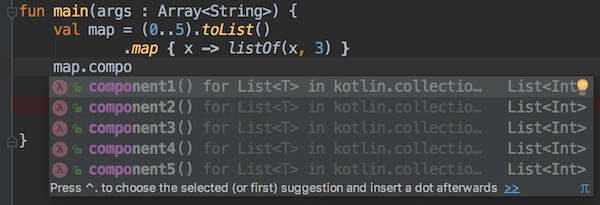
Kudos to the Kotlin team which make a language that feels functional with strategies that are very different to a “real” functional language. I have been an outsider to the JVM most of my time, but when you get to know Java and Kotlin I really cannot fathom what exactly would make you stick to Java.

Type safety vs elegance?

In order for ruby and Kotlin to shine in this example, both pay up by allowing misunderstandings in API use to surface only at runtime. Note that in both languages the compiler will happily allow you to capture more or less output than each_cons/windowed actually provides. This seems to be the price you need to pay for such an API, since the output “type” is determined by the argument to the windowing function. Now if there was a language where types could be determined programmatically…

Idris

Idris is a programming language which is close in spirit to Haskell but adds the capability to define dependent types.

Disclaimer: I have never worked with Idris before, I just had the vague idea that dependent types could be what I was looking for in this moment. Most of the things in Idris continue to be outside my grasp. Many, many thanks go out to Anton Trunov who answered my stackoverflow questions.

In this language, we can define the following type signature for a method:

window : (n : Nat) -> List a -> List (Vect n a)

This describes a method that takes a natural number n, and a list containing things with type a and then returns a list containing vectors of length n. n has now become part of the type definition for Vect. With much help (I couldn’t see how to make the leap from the variable length List a to the type Vect n a), this is then one possible implementation of windowed in Idris:

total
takeExact : (n : Nat) -> (xs : List a) -> Maybe (Vect n a)
takeExact Z xs = Just []
takeExact (S n) [] = Nothing
takeExact (S n) (x :: xs) with (takeExact n xs)
  takeExact (S n) (x :: xs) | Nothing = Nothing
  takeExact (S n) (x :: xs) | (Just v) = Just (x :: v)




total
window : (n : Nat) -> List a -> List (Vect n a)
window n xs with (takeExact n xs)
  window n xs | Nothing = []
  window n [] | (Just ys) = []
  window n (x :: xs) | (Just ys) = ys :: window n xs

total tells the Idris compiler to check the method whether it is indeed total as far as Idris is capable to tell. Total means that this method is guaranteed to return for whatever input that is provided. Z and S are types representing Zero and Successor within the Natural number type.

Now we can use the window function to write down the example provided.

--with
condition : Vect 2 Integer -> Bool
condition [x,y] = x == 0 && y == 1


*hello> length $ filter condition (window 2 $ 0::[1,2,3,4])
1 : Nat

It is also pretty compact, with the little difference that the filter function provided must deconstruct a Vector of type Vect 2 Integer, based on the arguments to the window function. That is, in your function you are forced to take the vector as a whole or deconstruct to exactly the right size that is provided.

Why is all this interesting? Because it is sometimes plain fun to compare different programming languages. They present to you different ways of thinking, different ways to express your intentions. One common theme is that conciseness comes when you get close to functional programming idioms. Also, before this post I didn’t think that you could actually expand upon the Haskell type system, but you can. Alas, we also have to recognize the great popularity of languages like ruby. Reasoning with types requires much practice, but help you squash bugs before you even get to the runtime. Languages like javascript and ruby reward you quickly when you get your act together, but depend on decent documentation to get API usage right.

Hence, ruby is indeed expressive, but quite a few popular languages have learned to recreate that expressiveness with the possibilities that their respective runtimes provide.